Monocular cues for depth perception

Monocular cues for depth perception

In our last post, we discussed how you can use the information from your two eyes to estimate the relative depth of objects in the visual field. Both vergence and binocular disparity provided cues to where objects were situated in depth relative some fixation point, allowing us to obtain some information about the 3D arrangement of objects in space. Clearly, two eyes are helpful in resolving the ambiguity that follows from projecting the light coming from a three-dimensional scene onto a two-dimensional surface. We said that this projection of light onto the retina made it much harder to make good guesses about depth from one image, and that using two images was a necessary step towards making it possible for you to recover this information from the retinal data. However, consider the picture below:

 

Figure 1 - A boid in some trees. Some things here look closer to you than others, but how do you tell that when you don't have binocular information to help you?

This image is a flat picture sitting on your screen, which means that your two eyes don’t end up with useful disparity information to make guesses about the 3D layout of these objects in the world. Nonetheless, my guess is that you have some ideas about what things in this image are closer to you than others. This must mean that there actually is some information in a single retinal image that tells you something about depth! In fact, there are multiple monocular depth cues that allow you make reasonable inferences about relative depth even if you don’t have two eyes to work with. We’ll discuss these here, describing these different cues using some important distinctions between where the information comes from and what you can use it for. Specifically:

• Cues can either be object-based, light-based, or geometric depending on the underlying source of the information that allows you to estimate depth.
• Cues can either provide ordinal or metric information about depth, which means that you either learn about the order of objects in depth (closest, next-closest, furthest, etc.) or you get an actual number that tells you about how far away something is, respectively.

A critical thing to remember about all of these cues is that like all attempts to reason about an underconstrained problem, our use of these cues relies on making assumptions about the nature of the solution, or the information we can use to estimate the property we’re interested in. All of these cues can easily lead us astray if those assumptions are violated, so keep careful track of what we’re assuming, why we’re assuming it, and how that assumption may turn out to be false.

Light-based cues to monocular depth

We’ll begin by talking about some light-based cues to depth. By calling these cues light-based, what I really mean is that we will be using some lawful properties of how light behaves as a function of how far away it’s coming from to make guesses about the depth of objects in a scene. Another way to put this is to say that because of these things that light does, objects that are far away tend to look different than objects that are closer in specific ways. That means we can use those changes in appearance to estimate how far away different objects are.

Scattering of light

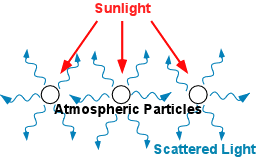
A great example of such a property of light is the tendency of light to scatter or change direction as it moves through a medium like the air in our atmosphere. By scattering, we mean pretty much exactly what you think: Light particles don’t just move straight through the air, but instead deviate from a straight path when they encounter molecules in the air or changes in density along their path (Figure 2). This simple fact ends up meaning that a lot of things happen to the way an object that is reflecting light looks if the light coming from it has to travel through more air to get to our eye. More air between our eye and the object means more opportunities to scatter, which changes multiple properties of that light as it makes its way towards us. For example:

Figure 2 - Light scatters when it encounters atmospheric particles. More air between you and an object means more opportunities to scatter.

• Light that scatters in random directions leads to edges that look blurry or fuzzy. Another way to say this is that the high spatial frequencies available in the pattern of light are reduced, leaving you with only coarse, low spatial frequency information.
• As light scatters more and more, you end up seeing increasingly equal amounts of light that actually came from the object and light that came from the background around it. Besides making edges blurry, this also reduces the difference between the brightness of the object relative to the brightness of the background, which is also known as the contrast of the object. Objects thus become harder and harder to distinguish from the background as distance increases.
• Light with shorter wavelengths (blue light) scatters more than light with longer wavelengths (red light). This means that light that comes from far away will tend to look more blue to you.

Running all of these cues backwards means that you can make the following guesses about an object’s depth based on its appearance: Objects that are blurrier, lower contrast, and more blue, are probably further away from you, just based on what probably happened to the light on its way to your eye from the object. Are these cues ordinal or metric? One thing to keep in mind is that while we can probably get a robust depth order out of these differences in appearance, actually guessing at the metric depth of an object will involve assuming a lot about the air between us and the object on a given day. The presence of particulate matter in the air, the temperature, and other environmental factors will change exactly how an object looks as a function of its distance. As it is, we’re also already assuming that objects don’t vary in how blue they are, how blurry or fuzzy they should look, and what their contrast is with the background! Regardless, these light-based cues are useful ways to make guesses about the relative depth of objects in the scene with information from one eye.

 

Figure 3 - A great example of aerial perspective. The faraway hills look fainter, blurrier, and bluer than the closer ridges and objects.

Shadows as a cue to depth

Another simple property of light that we can use to make guesses about depth is the presence of shadows in an image. Shadows can be cast or attached, meaning that the shadow lies on a surface that is separate from the object, or that the shadow lies on the surface of the object itself. In both cases, shadows can provide cues for depth. Cast shadows, for example, will look different as the distance between an object and a surface changes: (1) The size of the shadow relative to the object will change, (2) the blurriness of the shadow’s edges will change due to the diffraction of light around the edges of the object, and (3) The position of the shadow relative to the object may also change depending on the source of the light, and (4) The contrast between the shadow and the background may also tell you about the distance between the object and the surface. (Figure 4)

 Figure 4 - Fun with drop shadows in Powerpoint. As we manipulate the distance between the object and its cast shadow, the blurriness of the shadow, its size, and its contrast, we manipulate how far it appears to be floating above the surface below.

Attached shadows are also interesting cues to depth, but what they tell you about a scene tends to be somewhat different. Because attached shadows result from an object occluding itself from a light source, their appearance tends to tell you more about the object’s shape than about the distance between the object and another object or surface. This kind of shape is depth information, however, because understanding the 3D form of an object means understanding how different parts of the object are positioned in depth relative to one another. The inferences you make about object shape based on attached shadows tend to rely on a simple assumption, however, that is true a lot of the time but can be easily violated. Specifically, you tend to assume that light comes from above when interpreting shape using attached shadows. To see a simple demonstration of this, consider the figure below: Here, we’ve filled circles with the same transition between light and dark values, but flipped them upside-down on the right. This probably makes it look to you like the two sets of circles are either sticking out of the page (bumps) or sunk into the page (dents), because that’s how light from above would behave if those objects really were shaped that way. 

 

Figure 5 - Attached shadows signal 3D shape, and therefore depth. We assume that light comes from above, however, leading to different interpretations of these discs as bumps (left) or dents (right) if the same pattern is inverted.

In all of these cases, knowing some things about the way light behaves independently from our eye allows our visual system to make reasonable guesses about relative depth using the appearance of light coming from objects. Next, we’ll see how there are properties of the objects themselves that allow us to make similar guesses, but these also rely on critical assumptions regarding the things we’re looking at.

Object-based cues to depth

Our previous discussion of monocular depth cues focused on how light behaves when it has to come from further away, or when it interacts with objects at different depths. Next, we’ll consider a slightly different set of cues that are based on how object appearance may also change as depth relationships change in a complex scene. That is how do objects tend to look different when they are positioned further away from us than other objects? As above, these different cues all rest on different assumptions about the objects we’re looking at, which each represent opportunities for us to get the wrong estimate if those assumptions have been violated. These cues also differ in terms of whether we get ordinal or metric information out of the image. We’ll begin by considering a very simple object-based cue to depth.

Occlusion

How do objects at different distances from you tend to look different from one another? One very basic property of object appearance that tends to change with depth is the extent to which parts of an object are occluded, or blocked from view, by something that is between you and the object. Consider the simple shapes below, for example, and see which one you think is in front (Figure 6). My guess is that you’re pretty confident that the square is in front of the circle, because it looks like part of the circle is hidden from view behind the square. Simple, no? Occlusion is a very robust cue to monocular depth that provides an ordinal cue to object position in 3D. You can’t say exactly where the two objects are, but you can put them in some kind of order from closest to furthest.

Figure 6 - The square is probably in front of the circle. That is, as long as you're sure that it's a circle.

This relies on a simple assumption, though, that may seem so basic that you didn’t realize you were assuming it! In reasoning that the circle is further from you than the square, you “completed” the part of the circle that you couldn’t see. That is, you assumed that you were looking at an intact circle that happened to be behind a square rather than a ¾ circle that was positioned right against the edges of the square. We haven’t talked much about the way you make inferences like this about the shape of objects, but it’s worth saying that there’s a lot of evidence that you do. In most cases, you’re probably right about it, but all it takes is an irregularly shaped object to lead you down the wrong path. Even something as simple as object occlusion is based on assuming something to overcome the ambiguity in the data, which opens the door to error and misinterpretation.

Object size

Here’s another simple property of object appearance as a function of depth: Objects tend to take up less space on the retina as they get further away. Two objects that are the same size in the world will look smaller/larger than one another if they appear closer/further to you. If you happen to know the size of an object in the real world, you can even use a little bit of trigonometry to work out the distance between you and that object (Figure 7). That makes size potentially a metric cue to depth, but again, make sure you check your assumptions! The quality of your metric estimate will be directly related to the accuracy of your guess regarding the true size of the object – if you’re wrong about how big a car really is, for example, you’ll guess wrong about how far away it is. Even if you’re comparing objects that you’re unfamiliar with and trying to order them in depth, you’re still assuming something: namely that they’re likely to be about the same size in the real world! 

Figure 7 - The relationship between visual angle, object size, and distance allows us to estimate the distance to an object if we know its real size and the angle it subtends on the retina.

This matters a great deal when you use object size as a cue for interpreting things like texture patterns, because in this case the “objects” you’re working with are the texture elements that make up the pattern (the checks in a checkerboard, for example). You tend to assume that those elements are really the same size, leading to systematic guesses about the 3D layout of a scene or surface. If they’re not the same size, you’ll get the answer wrong, leading to distorted perceptions of distance or size. Below, you can see how bower birds tend to take advantage of these assumptions to make impressive-looking dens to try and charm potential mates with – by choosing object size and position carefully, the birds can manipulate the depth cues signaled by the texture gradient leading up to the nest, changing the interpretation of that object in their favor.

Figure 8 - When using object/texture element size to estimate depth relationships we tend to assume that similar-looking objects are the same physical size. This means that we can use regular patterns to estimate depth (left), but that this assumption can be challenged, leading to errors of depth perception and subsequent size perception (right).

Geometric cues to depth

Finally, I want to briefly discuss a set of cues that aren’t quite directly related to light nor directly related to objects, but more broadly affect the way objects in scenes tend to look as a function of distance. For lack of a better way to describe these, I’ll call these geometric cues to depth, because they’re primarily related to the way the projection of 3D scenes onto 2D surfaces tends to work regardless of whether we’re considering light independently or objects in particular.

            Though there are other cues we could talk about, I’m really going to focus here on one of these cues in particular: Linear perspective. My guess is that you have some familiarity with this cue, possibly from an art class you took at some point, but may need a bit of a refresher on the details. The most important thing for you to know about linear perspective is this: Lines that are really parallel in the world will meet at a vanishing point in the projection of that scene. Below is an example of a grid drawn with vanishing points in place to guide artists in rendering real-world parallel lines appropriately in an image.

 

Figure 9 - An empty grid with vanishing points used to establish linear perspective.

Linear perspective is a useful cue to depth because it allows us to link position in the image to depth in the world. For example, consider the simple illusion depicted below: My guess is that the monsters probably look like they’re different sizes to you, even though they’re physically the same size. What’s going on? You’re using the depth information provided by the converging lines in the scene to make inferences about which regions in the image are closer to you (the bottom left) and which regions are probably further from you (the center). This leads you to work out how big the objects must really be if they’re that far away and take up that much space, which in turn induces the illusory percept. Note the various assumptions that you’re making though: (1) The lines meet at that vanishing point because they’re really parallel, but receding in depth. (2) The position of the objects in the image faithfully reflects where they are in 3D – nothing is floating off of the ground, for example.  There’s more where those came from, but hopefully you get the gist: Like all of our  other cues, using linear perspective to infer depth depends on assumptions, any of which can be violated. One fantastic violation of these assumptions in particular is the Ames Room, which is a carefully constructed room that is built so that perspective relationships lead to a specific interpretation of the scene from a single vantage point (Figure 10). That interpretation leads you to make some incredibly wrong-headed inferences about object size, however, because of the way in which your assumptions about perspective are being challenged.

 Figure 10 - In the Ames Room, careful control of the vantage point and the way projected lines look from that position (left - public domain image from wikipedia) lead you to make erroneous estimates of depth that lead to misestimations of size (right - Image copyright: Tony Marsh)

Across the board then, you really can use just one eye (or monocular cues) to make guesses about relative depth. There’s lots of good information in scenes that provides hints about how objects and surfaces are positioned in 3D. The key is to never forget that these are guesses based on cues that aren’t perfect and that rely on assuming things about the world that might not be true. Regardless, some information is better than none, and your visual system tends to take what it can get.

We’ll continue to confront these kinds of issues as we move on to understanding our last “mid-level” property of visual perception – the perception of motion. Now would be a great time to do Lab #8 to acquaint yourself with some interesting phenomenology related to how you estimate the way things are moving based on how patterns of light change over time.